Page 106 - Propagation_antenne_adaptation

Comment ça marche ?

Radio-club F6KRK.
Les circuits réactifs

17 - Filtres complexes

Après les filtres gaussiens, nous allons poursuivre avec les filtres complexes dont la
fonction de transfert est issue de polynômes mathématiques particuliers.

EN QUÊTE DU FILTRE IDÉAL :
Avec les filtres gaussiens, on ne
peut guère descendre en dessous
d'un facteur de forme de 4 sans
pertes excessives (grand nombre
de pôles). Par contre, ils sont
faciles à régler et ils ont une phase
linéaire dans la bande passante.
Nous avons vu que l'on pouvait
améliorer le facteur de forme
avec des combinaisons de circuits
couplés. Le calcul et le réglage de
ces filtres deviennent vite « imbu-
vables ». Des mathématiciens ont
développé des polynômes particu-
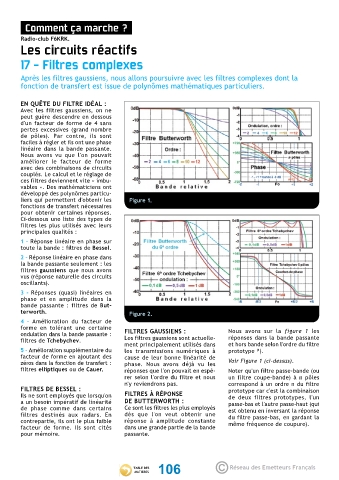
liers qui permettent d'obtenir les Figure 1.
fonctions de transfert nécessaires
pour obtenir certaines réponses.
Ci-dessous une liste des types de
filtres les plus utilisés avec leurs
principales qualités :
1 - Réponse linéaire en phase sur
toute la bande : filtres de Bessel.
2 - Réponse linéaire en phase dans
la bande passante seulement : les
filtres gaussiens que nous avons
vus (réponse naturelle des circuits
oscillants).
3 - Réponses (quasi) linéaires en
phase et en amplitude dans la
bande passante : filtres de But-
terworth. Figure 2.
4 - Amélioration du facteur de
forme en tolérant une certaine Nous avons sur la figure 1 les
ondulation dans la bande passante : FILTRES GAUSSIENS :
filtres de Tchebychev. Les filtres gaussiens sont actuelle- réponses dans la bande passante
ment principalement utilisés dans et hors bande selon l'ordre du filtre
5 - Amélioration supplémentaire du les transmissions numériques à prototype ).
(1
facteur de forme en ajoutant des cause de leur bonne linéarité de
zéros dans la fonction de transfert : phase. Nous avons déjà vu les Voir Figure 1 (ci-dessus).
filtres elliptiques ou de Cauer. réponses que l'on pouvait en espé- Noter qu'un filtre passe-bande (ou
rer selon l'ordre du filtre et nous un filtre coupe-bande) à n pôles
n'y reviendrons pas. correspond à un ordre n du filtre
FILTRES DE BESSEL : prototype car c'est la combinaison
Ils ne sont employés que lorsqu'on FILTRES À RÉPONSE de deux filtres prototypes, l'un
a un besoin impératif de linéarité DE BUTTERWORTH : passe-bas et l'autre passe-haut (qui
de phase comme dans certains Ce sont les filtres les plus employés est obtenu en inversant la réponse
filtres destinés aux radars. En dès que l'on veut obtenir une du filtre passe-bas, en gardant la
contrepartie, ils ont le plus faible réponse à amplitude constante même fréquence de coupure).
facteur de forme. Ils sont cités dans une grande partie de la bande
pour mémoire. passante.

106