Page 107 - Propagation_antenne_adaptation

FILTRES À RÉPONSE
DE TCHEBYCHEV :
On emploie ces filtres quand on
n'est pas trop exigeant sur la linéa-
rité de l'amplitude et de la phase
dans la bande passante. Ils per-
mettent pour un même facteur
de forme de réaliser le filtre avec
moins de pôles que pour le But-
terworth, donc (en principe) moins
de pertes. Voir sur la figure 2 un
exemple de filtre Tchebychev avec
trois ondulations différentes (filtre
prototype du 6 ème ordre et filtre
passe-bande 6 pôles).
Figure 3.
Voir Figure 2 (page précédente).
Noter que la bande relative se
réfère à la fréquence de transi-
tion et non plus à la fréquence de
coupure à -3 dB (voir annexe 1).
Nous pouvons voir sur la figure 2
qu'avec une ondulation de seule-
ment 0,1 dB, pour le même ordre,
il y a une nette amélioration du
facteur de forme du « Tchebychev »
par rapport au « Butterworth ».
Mais cela se paie par une ondula-
tion de phase dans la bande pas-
sante. Par ailleurs la réalisation
pratique demande un Q à vide des
composants bien plus élevé (ici, on
suppose qu'ils sont infinis).
FILTRES À RÉPONSE DE CAUER
(FILTRES ELLIPTIQUES) :
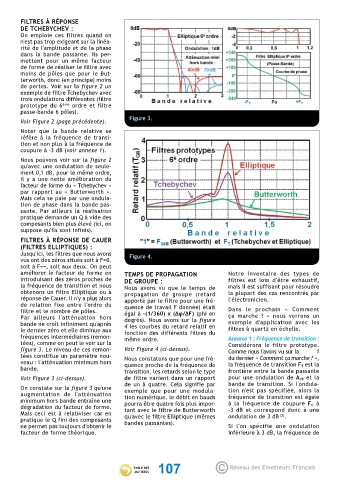
Jusqu'ici, les filtres que nous avons Figure 4.
vus ont des zéros situés soit à F=0,
soit à F=∞, soit aux deux. On peut
améliorer le facteur de forme en TEMPS DE PROPAGATION Notre inventaire des types de
introduisant des zéros proches de DE GROUPE : filtres est loin d'être exhaustif,
la fréquence de transition et nous Nous avons vu que le temps de mais il est suffisant pour résoudre
obtenons un filtre Elliptique ou à propagation de groupe (retard la plupart des cas rencontrés par
réponse de Cauer. Il n'y a plus alors apporté par le filtre pour une fré- l'électronicien.
de relation fixe entre l'ordre du quence de travail F donnée) était
filtre et le nombre de pôles. égal à -(1/360) x (Δφ/ΔF) (phi en Dans le prochain « Comment
Par ailleurs l'atténuation hors degrés). Nous avons sur la figure ça marche ? » nous verrons un
bande ne croît infiniment qu'après 4 les courbes du retard relatif en exemple d'application avec les
le dernier zéro et elle diminue aux fonction des différents filtres du filtres à quartz en échelle.
fréquences intermédiaires (remon- même ordre. Annexe 1 : Fréquence de transition :
tées), comme on peut le voir sur la Considérons le filtre prototype.
figure 3. Le niveau de ces remon- Voir Figure 4 (ci-dessus). Comme nous l'avons vu sur la ���1
tées constitue un paramètre nou- Nous constatons que pour une fré- du dernier « Comment ça marche ? »,
veau : l'atténuation minimum hors quence proche de la fréquence de la fréquence de transition F T est la
bande. transition, les retards selon le type frontière entre la bande passante
Voir Figure 3 (ci-dessus). de filtre varient dans un rapport pour une ondulation de A dB et la
de un à quatre. Cela signifie par bande de transition. Si l'ondula-
On constate sur la figure 3 qu'une exemple que pour une modula- tion n'est pas spécifiée, alors la
augmentation de l'atténuation tion numérique, le débit en bauds fréquence de transition est égale
minimum hors bande entraîne une pourra être quatre fois plus impor- à la fréquence de coupure F C à
dégradation du facteur de forme. tant avec le filtre de Butterworth -3 dB et correspond donc à une
Mais ceci est à relativiser car en qu'avec le filtre Elliptique (mêmes ondulation de 3 dB .
(2)
pratique le Q fini des composants bandes passantes).
ne permet pas toujours d'obtenir le Si l'on spécifie une ondulation
facteur de forme théorique. inférieure à 3 dB, la fréquence de

107