Page 57 - Propagation_antenne_adaptation

Comment ça marche ?

Par le radio-club F6KRK.
Les ellipsoïdes de Fresnel

En dehors des "hypermen", peu d'OM ont entendu parler des ellipsoïdes de Fresnel.
Nous espérons donc combler un manque avec cet article.

Considérons la figure 1. Pour tous les trajets situés à l’in- dégagé de plusieurs dizaines de
térieur ou entre deux ellipsoïdes, longueurs d’ondes.
les signaux arrivent plus ou moins Pour cela, il faut que les obstacles
déphasés avec le trajet princi- soient absents du premier ellip-
pal. Pour tous ceux situés sur les soïde de Fresnel. Mais attention,
ellipsoïdes, les signaux arrivent cela vaut pour les obstacles absor-
en opposition de phase pour ceux bants. Pour une surface réfléchis-
Figure 1 : d’ordre impair et en phase pour sante parallèle à l’axe E-R (sol),
ceux d’ordre pair. il convient de tenir compte, non
Nous avons un ellipsoïde ayant E Noter que les dimensions de l’el- seulement du premier ellipsoïde
et R comme foyers et un cercle de lipsoïde dépendent uniquement du de Fresnel, mais aussi de la largeur
révolution de rayon A, B. Celui-ci rapport entre la longueur d’onde du lobe de rayonnement qui, s’il
est maximum lorsque le point A se de la fréquence de travail et la dépasse l’angle dans lequel s’ins-
trouve à mi-chemin entre E et R. distance entre émetteur et récep- crit l’ellipsoïde, va permettre une
Soit B un point de l’ellipse. Les pro- teur, selon la formule : réflexion en opposition de phase si
priétés de celle-ci sont telles qu’en la hauteur des antennes est égale
tous ses points, la différence entre au demi-cercle de l’ellipsoïde
les trajets {E, A, R} et {E, B, R} est d’ordre impair. C’est pourquoi, la
une constante (cette propriété est r = rayon de l’ellipsoïde d’ordre 1, hauteur des antennes sera de pré-
utilisée pour tracer une ellipse avec d = distance entre E et R. férence égale au rayon d’un ellip-
deux épingles, un �l et un crayon). Pour �xer les ordres de grandeur, soïde d’ordre pair.
Cette différence reste constante avec une distance de 20 km, pour En pratique, l’ellipsoïde de Fres-
pour tout l’ellipsoïde. F = 10 GHz, r = 12 m et pour nel n’est pris en compte que pour
Soient E un émetteur et R un récep- F = 144 MHz, r = 102 m. des liaisons fixes hyperfréquences
teur, et considérons deux différents (faisceaux hertziens). Pour
trajets possibles pour une onde, LIAISON EN VISIBILITÉ. celles-ci, les distances, les lon-
soit en direct de E à R, soit avec Une liaison est dite en visibilité gueurs d’ondes et les largeurs des
ré�exion en un point de l’ellipsoïde. lorsque le signal se propage entre lobes de rayonnement permettent
Avec un signal ayant une longueur l’émetteur et le récepteur comme de respecter physiquement les cri-
d’onde λ, on peut déterminer une s’ils étaient en espace totalement tères de visibilité.
dimension {A, B} telle que la dif-
férence de trajet soit égale à λ/2.
Cette dimension correspond à un
ellipsoïde de Fresnel d’ordre 1. On
peut déterminer une autre dimen-
sion de {A, B} pour avoir une dif-
férence de trajet de 2λ/2, et un
ellipsoïde d’ordre 2. Et ainsi de
suite pour un ellipsoïde d’ordre n.
Voir sur la �gure 2 les deux pre-
miers ellipsoïdes de Fresnel.

Figure 2 :

La différence de longueur entre
{E, B, R} et {E, A, R} est identique
à celle entre {E, A, R} et {E, R},
soit λ/2.
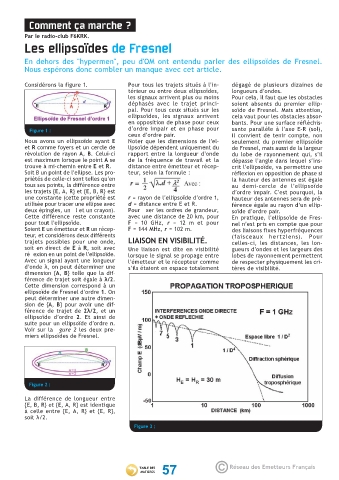
Figure 3 :

57

L754_000000_RADIOREF_JUILLET.indd 40 11/07/13 16:44