Page 38 - Antennes_hf2

En fait, on jette un voile pudique En électricité, les seules grandeurs
sur les phénomènes réels, trop
compliqués à analyser, et on dit
« il y a eu réflexion ».
Pour illustrer cela, il suffirait de
visualiser ce que subit une balle
de golf réfléchie sur un mur.
Rendre compte pratiquement
d’un phénomène aussi compliqué
étant impossible, on se contente
de constater « l’état avant » et
« l’état après » et de se dire
« il y a eu réflexion ».
5 – Dans une ligne à ROS différent
de 1, la répartition des intensités
et des tensions est sinusoïdale.
Faux. Elle est périodique, certes,
mais pas sinusoïdale. Les minima
sont plus « pincés » que les
maxima. Il n’y a que dans le cas
où le ROS est infini que la courbe
devient sinusoïdale, et donc que
les calculs se simplifient.
6 – Entre émetteur et antenne, la
décomposition de l'onde en onde
directe et onde réfléchie corres-
pond à une réalité physique, cha-
cune de ces ondes transportant
de la puissance, l'une de l'émet-
teur vers l'antenne, l'autre de
l'antenne vers l'émetteur.
Faux. Cette décomposition, bien
pratique pour analyser les phé-
nomènes, est purement mathé-
matique, et la seule puissance
réellement transportée l'est de son
lieu de génération (l'émetteur) vers
son lieu de consommation (l'antenne).
On peut s'en convaincre en consi-
dérant le cas-limite d'une ligne
où le ROS est infini : elle n'est
le siège d'aucun déplacement de
puissance, et pas celui d'un dépla- plus constantes le long de la ligne
cement de puissance dans un sens
et d'un déplacement égal dans
l'autre sens.
F5NB : F6FQX poursuit en donnant
trois exemples (démonstrations)
mathématiques qui conduisent aux
mêmes résultats (puissance trans-
mise, impédances, etc.) mais cha-
cun avec des puissances directes et
réfléchies (ou puissance apparente
et puissance réactive) différentes .
[1]
Il ne peut y avoir plusieurs valeurs
pour un même phénomène phy-
sique. Cette approche mathéma-
tique complète étant indigeste
pour la plupart des OM (y com-
pris moi-même) je vais tenter une
approche basée sur le raisonne-
ment avec simplification de la
partie mathématique.
Le rapport entre Umax et Umin et
que l'on peut puisse mesurer sont entre Imax et Imin (le même) est
la tension et l'intensité. exprimé par le ROS (Rapport d'Ondes
Ensuite il suffit de les multiplier Stationnaires), valeur très importante
(4)
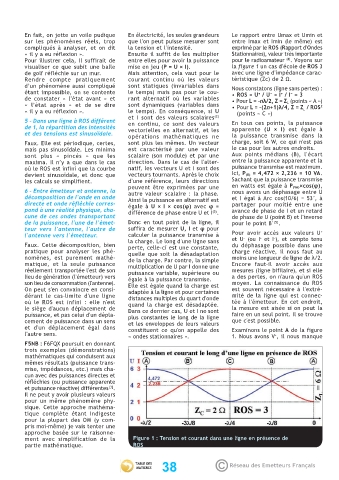
entre elles pour avoir la puissance pour le radioamateur . Voyons sur
mise en jeu (P = U × I). la figure 1 un cas d'école de ROS 3
Mais attention, cela vaut pour le avec une ligne d'impédance carac-
courant continu où les valeurs téristique (Zc) de 2 Ω.
sont statiques (invariables dans Nous constatons (ligne sans pertes) :
le temps) mais pas pour le cou- • ROS = U / U = I / I = 3
+
−
+
−
rant alternatif où les variables • Pour L = -nλ/2, Z = Z L (points « A »)
sont dynamiques (variables dans • Pour L = -(2n+1)λ/4, Z = Z / ROS 2
le temps). En conséquence, si U (points « C ») L
et I sont des valeurs scalaires (2)
en continu, ce sont des valeurs En tous ces points, la puissance
vectorielles en alternatif, et les apparente (U × I) est égale à
opérations mathématiques ne la puissance transmise dans la
sont plus les mêmes. Un vecteur charge, soit 6 W, ce qui n'est pas
est caractérisé par une valeur le cas pour les autres endroits.
scalaire (son module) et par une Aux points médians (B), l'écart
direction. Dans le cas de l'alter- entre la puissance apparente et la
natif, les vecteurs U et I sont des puissance transmise est maximum.
vecteurs tournants. Après le choix Ici, P (B) = 4,472 × 2,236 = 10 VA.
d'une référence, leurs directions Sachant que la puissance transmise
peuvent être exprimées par une en watts est égale à P (VA)×cos(φ),
autre valeur scalaire : la phase. nous avons un déphasage entre U
Ainsi la puissance en alternatif est et I égal à Arc cos(10/6) = 53°, à
égale à U × I × cos(φ) avec φ = partager pour moitié entre une
différence de phase entre U et I . avance de phase de I et un retard
(3)
de phase de U (point B) et l'inverse
Donc en tout point de la ligne, il pour le point B' .
(5)
suffira de mesurer U, I et φ pour +
calculer la puissance transmise à Pour avoir accès aux valeurs U
+
−
−
la charge. Le long d'une ligne sans et U (ou I et I ), et compte tenu
perte, celle-ci est une constante, du déphasage possible dans une
quelle que soit la désadaptation charge réactive, il nous faut au
de la charge. Par contre, la simple moins une longueur de ligne de λ/2.
multiplication de U par I donne une Encore faut-il avoir accès aux
puissance variable, supérieure ou mesures (ligne bifilaire), et si elle
égale à la puissance transmise. a des pertes, on n'aura qu'un ROS
Elle est égale quand la charge est moyen. La connaissance du ROS
adaptée à la ligne et pour certaines est souvent nécessaire à l'extré-
distances multiples du quart d'onde mité de la ligne qui est connec-
quand la charge est désadaptée. tée à l'émetteur. En cet endroit,
Dans ce dernier cas, U et I ne sont la mesure est aisée si on peut la
faire en un seul point. Il se trouve
et les enveloppes de leurs valeurs que c'est possible.
constituent ce qu'on appelle des Examinons le point A de la figure
« ondes stationnaires ». 1. Nous avons V , il nous manque
+
Figure 1 : Tension et courant dans une ligne en présence de
ROS
38