Page 34 - CCM_LignesHF

Comment ça marche ?

Radio-club F6KRK
Les lignes HF

14 - Adaptation par lignes (2)

Après avoir vu plusieurs exemples d'adaptation à l'aide de lignes employées en trans-
mission, nous allons continuer l'adaptation avec des lignes utilisées en remplacement de
composants réactifs passifs.

SYNTHÈSE DES BOBINES ET On pourrait croire qu'elle soit propor- Utilisation de l'abaque : lorsqu'on a la
DES CONDENSATEURS. tionnelle à la longueur de la ligne, valeur du composant (L ou C) à syn-
Utilisation de lignes ouvertes et mais cela ne serait le cas qu'en courant thétiser, on calcule une longueur ini-
fermées de longueurs < λ/4. continu. tiale pour la ligne en divisant la valeur
désirée par la constante linéique de
Pour simplifier, nous supposerons que Pour comprendre la loi de variation la ligne. On reporte cette longueur
les pertes dans la ligne sont négli- de la valeur équivalente, il suffit de sur l'abaque et on lit le facteur multi-
geables, ce qui peut être admis pour se souvenir qu'elle est le résultat de plicatif. Alors on diminue la longueur
une longueur inférieure au quart l'addition des deux réactances pré- pour retrouver la valeur recherchée,
d'onde. sentées par la ligne, réactances liées facteur multiplicatif compris. Cela ne
Nous avons vu qu'une ligne était com- à la capacité linéique C et à la self demande que quelques itérations.
1
posée d'une self linéique L et d'une linéique L , soit : APPLICATION À L'ACCORD
1
1
capacité linéique C . Quand la ligne X = (+X ) + (- X ) D'UNE ANTENNE.
1
est infinie, ou si elle est chargée L C Nous allons nous intéresser à un cas
par son impédance caractéristique, avec particulier où la partie réelle de
quelle que soit sa longueur L, les L = L × L et C = C × L. l'impédance d'antenne a une valeur
réactances de sa self L = L × L et 1 1 inférieure aux 50 Ω du câble coaxial.
1
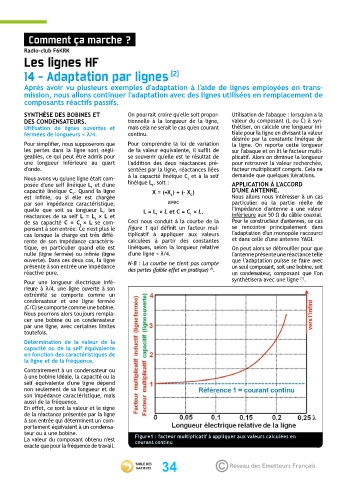
de sa capacité C = C × L se com- Ceci nous conduit à la courbe de la Pour le constructeur d'antennes, ce cas
1
pensent à son entrée. Ce n'est plus le figure 1 qui définit un facteur mul- se rencontre principalement dans
cas lorsque la charge est très diffé- tiplicatif à appliquer aux valeurs l'adaptation d'un monopôle raccourci
rente de son impédance caractéris- calculées à partir des constantes et dans celle d'une antenne YAGI.
tique, en particulier quand elle est linéiques, selon la longueur relative On peut alors se débrouiller pour que
nulle (ligne fermée) ou infinie (ligne d'une ligne < λ/4. l'antenne présente une réactance telle
ouverte). Dans ces deux cas, la ligne N-B : La courbe ne tient pas compte que l'adaptation puisse se faire avec
présente à son entrée une impédance (1) un seul composant, soit une bobine, soit
réactive pure. des pertes (faible effet en pratique) . un condensateur, composant que l'on
[1]
Pour une longueur électrique infé- synthétisera avec une ligne .
rieure à λ/4, une ligne ouverte à son
extrémité se comporte comme un
condensateur et une ligne fermée
(C/C) se comporte comme une bobine.
Nous pourrons alors toujours rempla-
cer une bobine ou un condensateur
par une ligne, avec certaines limites
toutefois.
Détermination de la valeur de la
capacité ou de la self équivalente
en fonction des caractéristiques de
la ligne et de la fréquence.
Contrairement à un condensateur ou
à une bobine idéale, la capacité ou la
self équivalente d'une ligne dépend
non seulement de sa longueur et de
son impédance caractéristique, mais
aussi de la fréquence.
En effet, ce sont la valeur et le signe
de la réactance présentée par la ligne
à son entrée qui déterminent un com-
portement équivalent à un condensa-
teur ou à une bobine.
La valeur du composant obtenu n'est Figure1 : facteur multiplicatif à appliquer aux valeurs calculées en
courant continu
exacte que pour la fréquence de travail.
34