Page 28 - Propagation_antenne_adaptation
P. 28
L'avantage de cette approche est de pouvoir calculer facile- 'JHVSF O
ment le diagramme de rayonnement vertical pour tous les
Wd]b[i Z _dY_Z[dY[$ ;nWc_dedi bW \_]kh[ *$
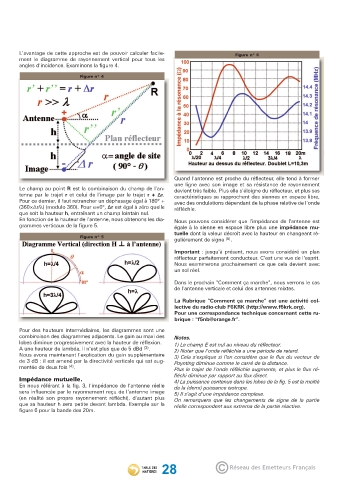
'JHVSF O
GkWdZ b Wdj[dd[ [ij fheY^[ Zk h\b[Yj[kh" [bb[ j[dZ } \ehc[h
une ligne avec son image et sa résistance de rayonnement
Le champ au point R est la combinaison du champ de l'an- devient très faible. Plus elle s'éloigne du réflecteur, et plus ses
tenne par le trajet r et celui de l'image par le trajet r + ∆r. caractéristiques se rapprochent des siennes en espace libre,
Fekh Y[ Z[hd_[h" _b \Wkj h[jhWdY^[h kd Zf^WiW][ ]Wb } '.& !
avec des ondulations dépendant de la phase relative de l'onde
),& »h%h ceZkbe ),& $ Fekh _3&" ∆r est égal à zéro quelle
réfléchie.
que soit la hauteur h, entraînant un champ lointain nul.
En fonction de la hauteur de l'antenne, nous obtenons les dia- Deki fekledi Yedi_Zh[h gk[ b _cfZWdY[ Z[ b Wdj[dd[ [ij
grammes verticaux de la figure 5. égale à la sienne en espace libre plus une impédance mu-
tuelle dont la valeur décroît avec la hauteur en changeant ré-
'JHVSF O
(5)
gulièrement de signe .
Important : jusqu'à présent, nous avons considéré un plan
réflecteur parfaitement conducteur. C'est une vue de l'esprit.
Deki [nWc_d[hedi fheY^W_d[c[dj Y[ gk[ Y[bW Z[l_[dj Wl[Y
un sol réel.
:Wdi b[ fheY^W_d 9ecc[dj W cWhY^[ " deki l[hhedi b[ YWi
de l'antenne verticale et celui des antennes mixtes.
La Rubrique "Comment ça marche" est une activité col-
lective du radio-club F6KRK (http://www.f6krk.org).
Pour une correspondance technique concernant cette ru-
brique : "f5nb@orange.fr".
Pour des hauteurs intermédiaires, les diagrammes sont une
combinaison des diagrammes adjacents. Le gain au maxi des Notes.
lobes diminue progressivement avec la hauteur de réflexion. 1) Le champ E est nul au niveau du réflecteur.
(3)
7 kd[ ^Wkj[kh Z[ bWcXZW" _b d [ij fbki gk[ Z[ + Z8Z . 2) Noter que l'onde réfléchie a une période de retard.
Deki Wledi cW_dj[dWdj b [nfb_YWj_ed Zk ]W_d ikffbc[djW_h[ 3) Cela s'explique si l'on considère que le flux du vecteur de
Z[ ) Z8 0 _b [ij Wc[d fWh bW Z_h[Yj_l_j l[hj_YWb[ gk_ [ij Wk]# Poynting diminue comme le carré de la distance.
*
mentée de deux fois .
Plus le trajet de l'onde réfléchie augmente, et plus le flux ré-
fléchi diminue par rapport au flux direct.
*NQnEBODF NVUVFMMF 4) La puissance contenue dans les lobes de la fig. 5 est la moitié
En nous référant à la fig. 3, l'impédance de l'antenne réelle de la (demi) puissance isotrope.
i[hW _d\bk[dY[ fWh b[ hWoedd[c[dj h[k Z[ b Wdj[dd[ _cW][
5) Il s'agit d'une impédance complexe.
(en réalité son propre rayonnement réfléchi), d'autant plus On remarquera que les changements de signe de la partie
que sa hauteur h sera petite devant lambda. Exemple sur la réelle correspondent aux extrema de la partie réactive.
\_]kh[ , fekh bW XWdZ[ Z[i (&c$
28