Page 71 - Propagation_antenne_adaptation

Comment ça marche ?

Radio-club F6KRK.
Les circuits réactifs

1 - La réactance

Nous nous donnerons pour but, en analysant le comportement des composants réactifs
fondamentaux que sont les condensateurs et les bobines, d'arriver à la notion de réac-
tance sans recourir à de savantes mathématiques.

LE CONDENSATEUR EN CONTINU. En considérant les valeurs crêtes Q : Quelle est l'allure de la tension ?
La charge d'un condensateur à crêtes pendant la durée T, nous R : Pour répondre, il faudra quand
connecté à une source de tension remarquons que : même faire un peu de maths.
est régie par l'équation suivante : l la valeur crête à crête de la ten- Un matheux aura vu que dans la
Q = C × U, avec Q = charge en sion est 2 fois plus faible que formule donnant la tension U,
Coulombs, C = capacité en Farads celle qu'elle aurait si le courant celle-ci est en fait obtenue par
et U = tension de la source en Volts. ne changeait pas de sens (elle cor- intégration du courant par rapport
Nous avons par ailleurs I = Q / t, respond à une durée de T/2) ; au temps. Autrement dit, la fonction
c'est-à-dire que l'intensité d'un cou- l par ailleurs, la valeur du courant de U est la primitive de la fonction
rant en ampères est égale à son crête est multipliée par 2 (± I). de I. Quand I est une constante, U
er
débit en coulombs par seconde. La formule donnant U crête à crête est une fonction du 1 degré, c'est-
En combinant ces égalités et en est alors la suivante : à-dire une droite oblique. Quand
connectant notre condensateur à I est une fonction sinusoïdale,
une source de courant constant, sa primitive U est une fonction
la tension U en volts développée à cosinusoïdale car la primitive de
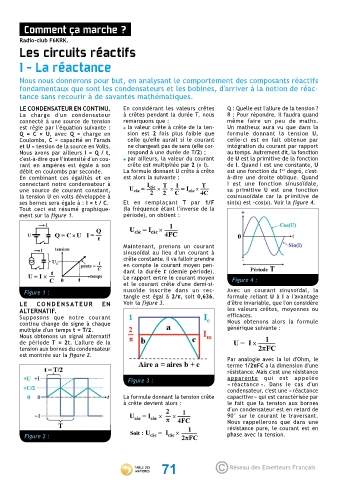
ses bornes sera égale à : I × t / C. Et en remplaçant T par 1/F sin(x) est -cos(x). Voir la figure 4.
Tout ceci est résumé graphique- (la fréquence étant l'inverse de la
ment sur la figure 1. période), on obtient :

Maintenant, prenons un courant
sinusoïdal au lieu d'un courant à
crête constante. Il va falloir prendre
en compte le courant moyen pen-
dant la durée t (demie période).
Le rapport entre le courant moyen Figure 4 :
et le courant crête d'une demi-si-
Figure 1 : nusoïde inscrite dans un rec- Avec un courant sinusoïdal, la
tangle est égal à 2/π, soit 0,636. formule reliant U à I a l'avantage
L E CO N D E NS AT EU R E N Voir la figure 3. d'être invariable, que l'on considère
ALTERNATIF. les valeurs crêtes, moyennes ou
Supposons que notre courant efficaces.
continu change de signe à chaque Nous obtenons alors la formule
multiple d'un temps t = T/2. générique suivante :
Nous obtenons un signal alternatif
de période T = 2t. L'allure de la
tension aux bornes du condensateur
est montrée sur la figure 2.
Par analogie avec la loi d'Ohm, le
terme 1/2πFC a la dimension d'une
résistance. Mais c'est une résistance
Figure 3 : apparente qui est appelée
« réactance ». Dans le cas d'un
condensateur, c'est une « réactance
La formule donnant la tension crête capacitive » qui est caractérisée par
à crête devient alors : le fait que la tension aux bornes
d'un condensateur est en retard de
90° sur le courant le traversant.
Nous rappellerons que dans une
résistance pure, le courant est en
Figure 2 : phase avec la tension.

71