Page 27 - CCM_LignesHF

Comment ça marche ?

Radio-club F6KRK
Les lignes HF

11 - Impédance (3)

Après avoir vu les impédances le long d'une ligne et les relations « complexes » qui les
relient à la charge, nous allons examiner les effets de certaines combinaisons ligne /
composants L-C en nous aidant de l'abaque de Smith.

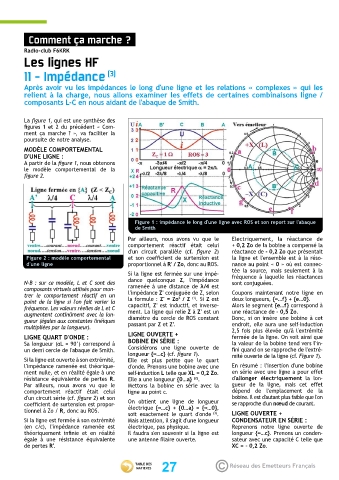
La figure 1, qui est une synthèse des
figures 1 et 2 du précédent « Com-
ment ça marche ? », va faciliter la
poursuite de notre analyse.
MODÈLE COMPORTEMENTAL
D'UNE LIGNE :
A partir de la figure 1, nous obtenons
le modèle comportemental de la
figure 2.

Figure 1 : impédance le long d'une ligne avec ROS et son report sur l'abaque
de Smith

Par ailleurs, nous avons vu que le Electriquement, la réactance de
comportement réactif était celui + 0,2 Zo de la bobine a compensé la
d'un circuit parallèle (cf. figure 2) réactance de - 0,2 Zo que présentait
Figure 2 : modèle comportemental et son coefficient de surtension est la ligne et l'ensemble est à la réso-
d'une ligne proportionnel à R' / Zo, donc au ROS. nance au point « 0 » où est connec-
tée la source, mais seulement à la
Si la ligne est fermée sur une impé- fréquence à laquelle les réactances
N-B : sur ce modèle, L et C sont des dance quelconque Z, l'impédance sont conjuguées.
composants virtuels utilisés pour mon- ramenée à une distance de λ/4 est
trer le comportement réactif en un l'impédance Z' conjuguée de Z, selon Coupons maintenant notre ligne en
2
(1)
point de la ligne si l'on fait varier la la formule : Z' = Zo / Z . Si Z est deux longueurs, {∞…f} + {e…0}.
fréquence. Les valeurs réelles de L et C capacitif, Z' est inductif, et inverse- Alors le segment {e…f} correspond à
augmentent continûment avec la lon- ment. La ligne qui relie Z à Z' est un une réactance de - 0,5 Zo.
gueur (égales aux constantes linéiques diamètre du cercle de ROS constant Donc, si on insère une bobine à cet
multipliées par la longueur). passant par Z et Z'. endroit, elle aura une self-induction
2,5 fois plus élevée qu'à l'extrémité
LIGNE OUVERTE +
LIGNE QUART D'ONDE : fermée de la ligne. On voit ainsi que
Sa longueur (αL = 90°) correspond à BOBINE EN SÉRIE : la valeur de la bobine tend vers l'in-
un demi cercle de l'abaque de Smith. Considérons une ligne ouverte de fini quand on se rapproche de l'extré-
longueur {∞…c} (cf. figure 1). mité ouverte de la ligne (cf. Figure 1).
Si la ligne est ouverte à son extrémité, Elle est plus petite que le quart
l'impédance ramenée est théorique- d'onde. Prenons une bobine avec une En résumé : l'insertion d'une bobine
ment nulle, et en réalité égale à une self-induction L telle que XL = 0,2 Zo. en série avec une ligne a pour effet
résistance équivalente de pertes R. Elle a une longueur {0…a} . d'allonger électriquement la lon-
(2)
Par ailleurs, nous avons vu que le Mettons la bobine en série avec la gueur de la ligne, mais cet effet
comportement réactif était celui ligne au point c. dépend de l'emplacement de la
d'un circuit série (cf. figure 2) et son bobine. Il est d'autant plus faible que l'on
coefficient de surtension est propor- On obtient une ligne de longueur se rapproche d'un nœud de courant.
tionnel à Zo / R, donc au ROS. électrique {∞…c} + {0…a} = {∞…0},
soit exactement le quart d'onde . LIGNE OUVERTE +
(3)
Si la ligne est fermée à son extrémité Mais attention, il s'agit d'une longueur CONDENSATEUR EN SÉRIE :
(en c/c), l'impédance ramenée est électrique, pas physique. Reprenons notre ligne ouverte de
théoriquement infinie et en réalité Il faudra s'en souvenir si la ligne est longueur {∞…c}. Prenons un conden-
égale à une résistance équivalente une antenne filaire ouverte. sateur avec une capacité C telle que
de pertes R'. XC = - 0,2 Zo.

27